nLab balanced monoidal category

Definition

A twist, or balance, in a braided monoidal category $\mathscr{C}$ is a natural isomorphism $\theta$ from the identity functor on $\mathscr{C}$ to itself satisfying the following compatibility condition with the braiding $\beta$:

$$\theta_{A\otimes B} \;=\; \beta_{B,A} \circ \beta_{A,B} \circ (\theta_A \otimes \theta_B), \,\, \forall A, B \in \mathscr{C}$$

A balanced monoidal category is a braided monoidal category equipped with such a balance.

Beware that there is an un-related notion of balanced categories.

Properties

In the language of string diagrams, the balancing is represented by a 360-degree twist:

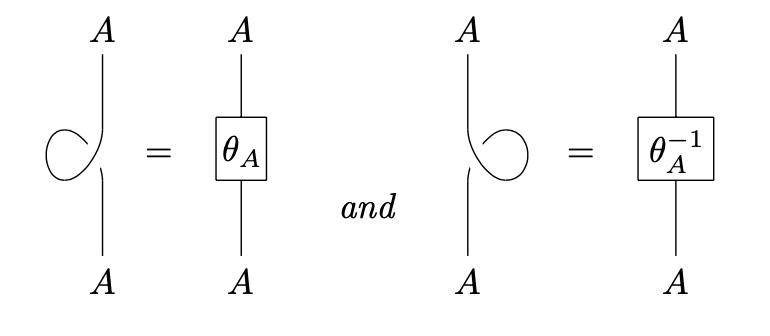
Every symmetric monoidal category is balanced in a canonical way. In fact, the identity natural transformation on the identity functor of $\mathscr{C}$ is a balance on $\mathscr{C}$. In this way, the twist can be seen as a way of “controlling” the non-symmetric behavior of the braiding.

A braided rigid monoidal category is balanced if and only if it is a pivotal category, but a balanced monoidal category need not be rigid (cf. Selinger 2011, Lem. 4.20).

References

The original definition:

• André Joyal, Ross Street, The geometry of tensor calculus I, Adv. Math. 88 1 (1991) 55–112, [doi:10.1016/0001-8708(91)90003-P]

The above definition follows:

• Jeff Egger, Appendix C in: Of Operator Algebras and Operator Spaces (2006) [pdf]

See also:

• Peter Selinger, A survey of graphical languages for monoidal categories,

  Springer Lecture Notes in Physics 813 (2011) 289-355 [arXiv:0908.3347, doi:10.1007/978-3-642-12821-9_4]